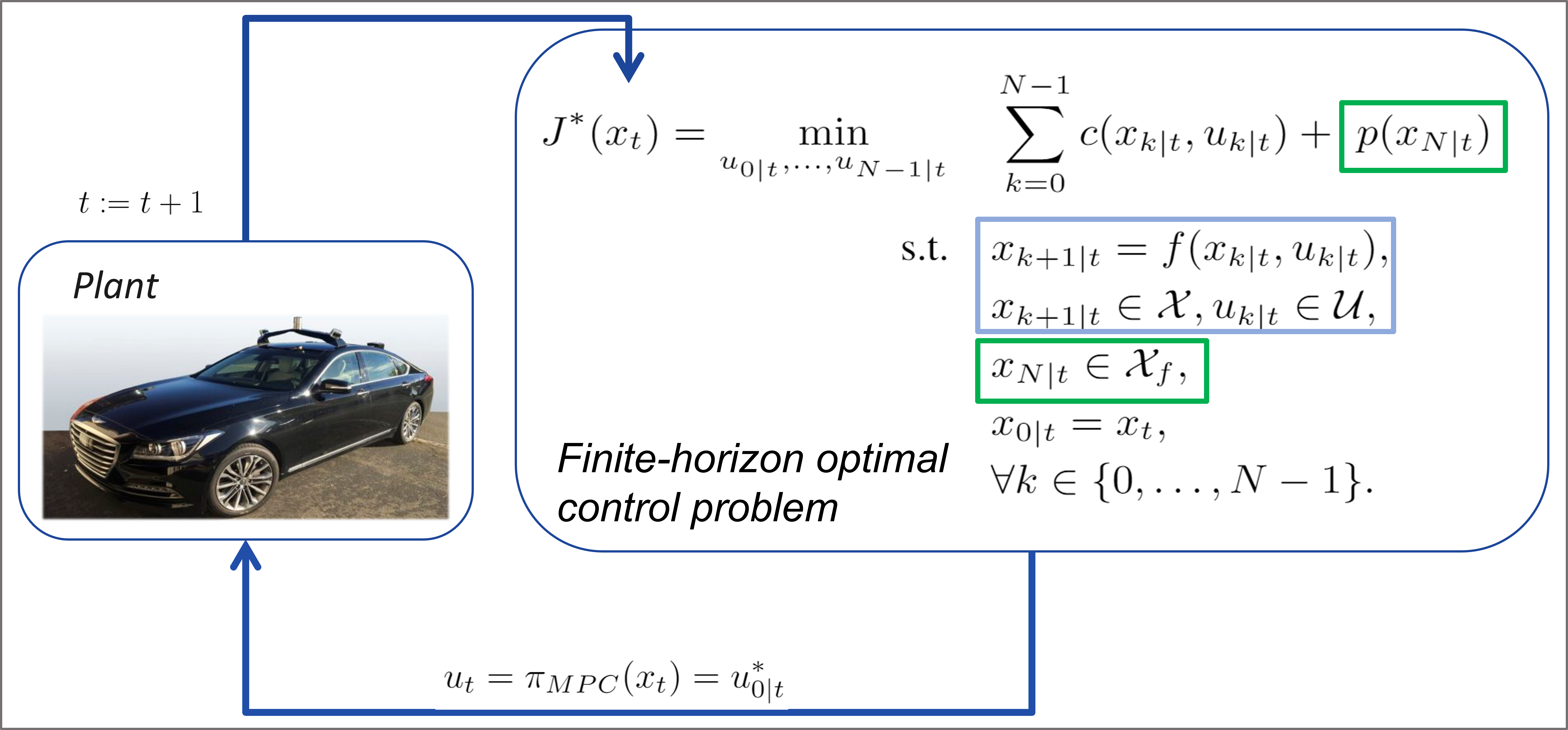
Data-driven Nonlinear MPC
Using trajectory traces of nonlinear systems for designing robust MPC with guarantees
In this project, we develop data-driven MPC for constrained optimal control of nonlinear systems with a specific emphasis on safety, performance and computational efficiency.
Towards safety, we propose a non-parametric technique to construct prediction models for nonlinear systems with Lipschitz/Lur’e unmodelled dynamics. We use set membership to approximate the graph (in the set-theoretic sense) of the unknown function via semidefinite programming using incremental quadratic constraints.
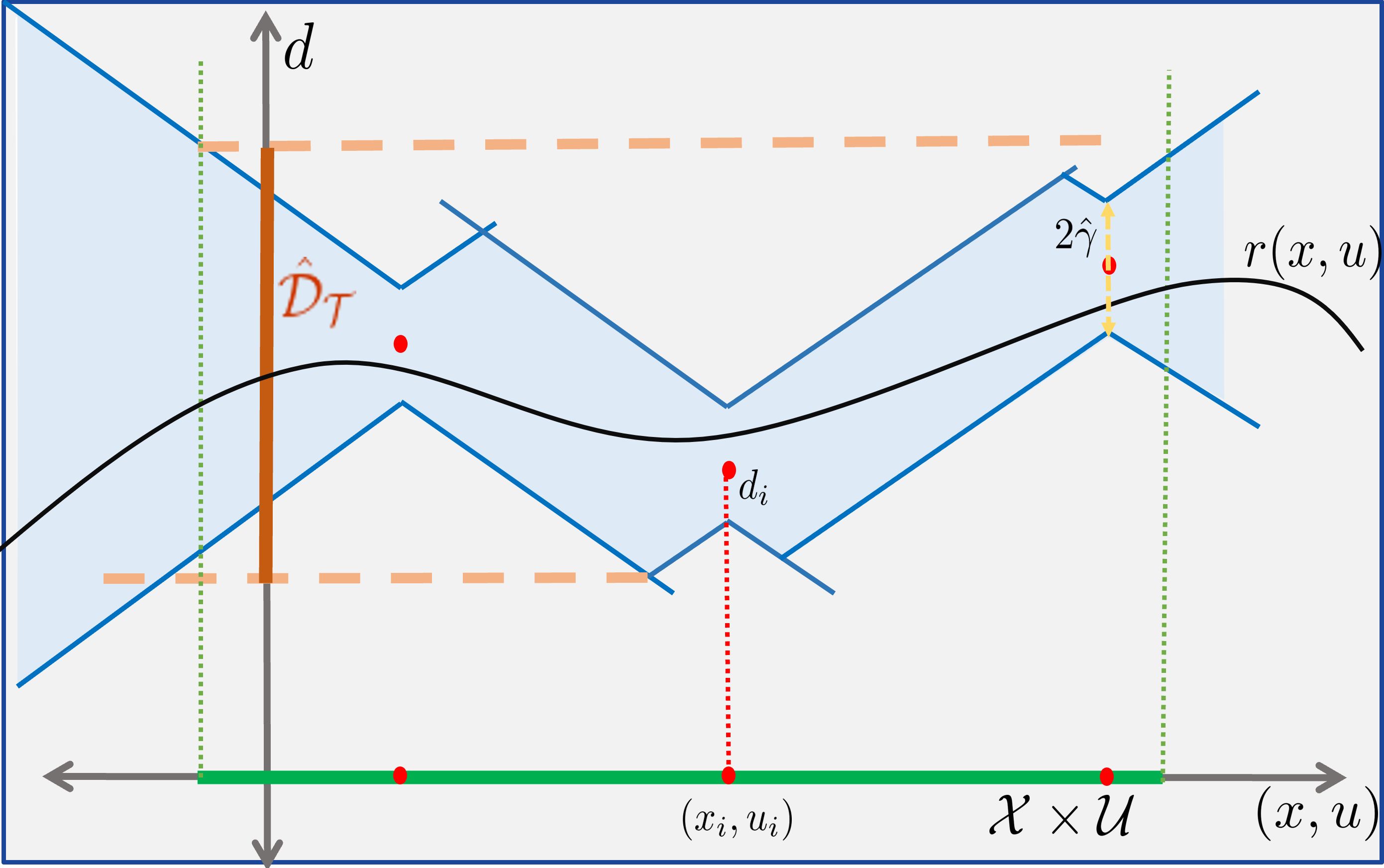
This technique has been used for (I) computation of tractable bounds for unmodelled dynamics, (II) computation of positive invariant sets and (III) adaptive constraint tightening for adaptive MPC
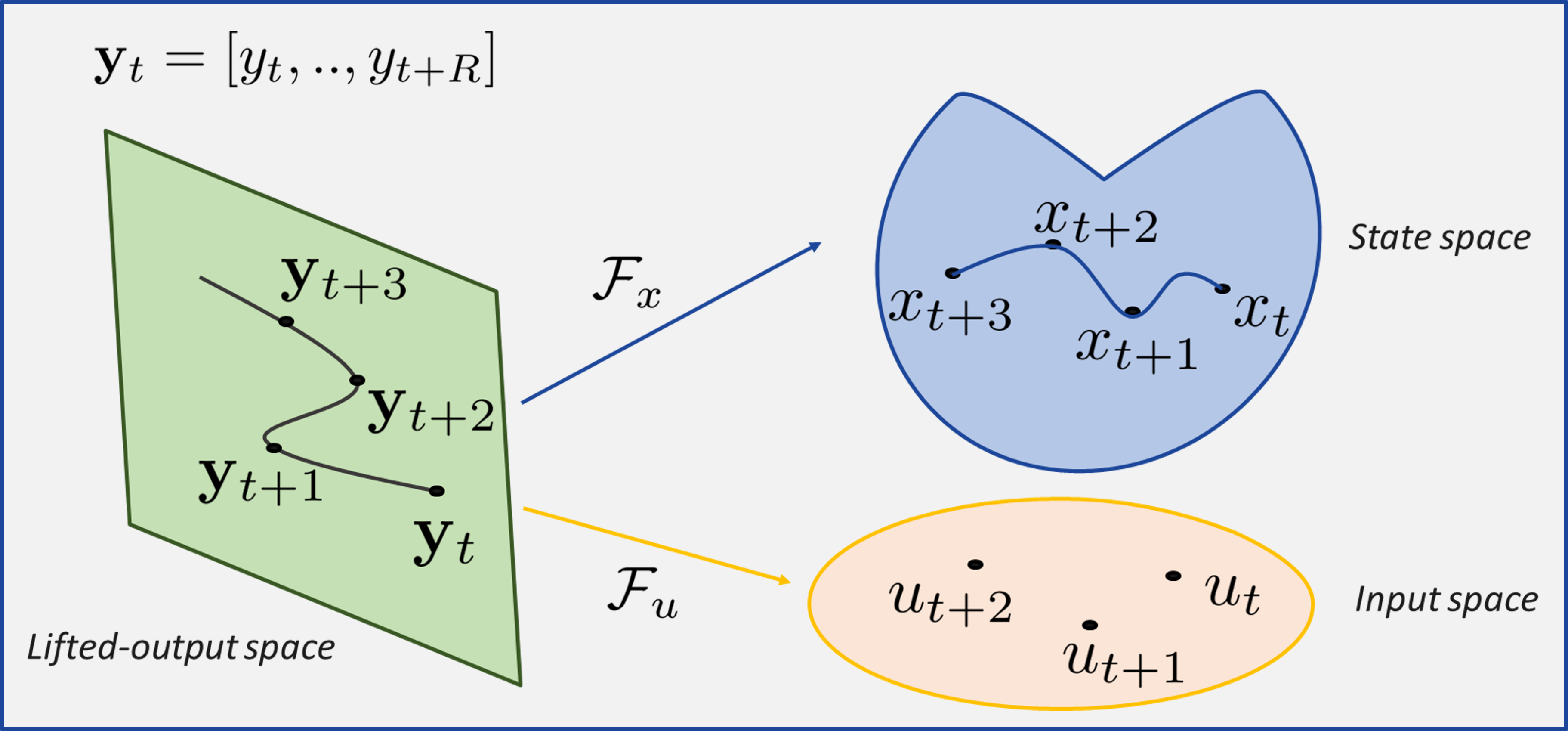
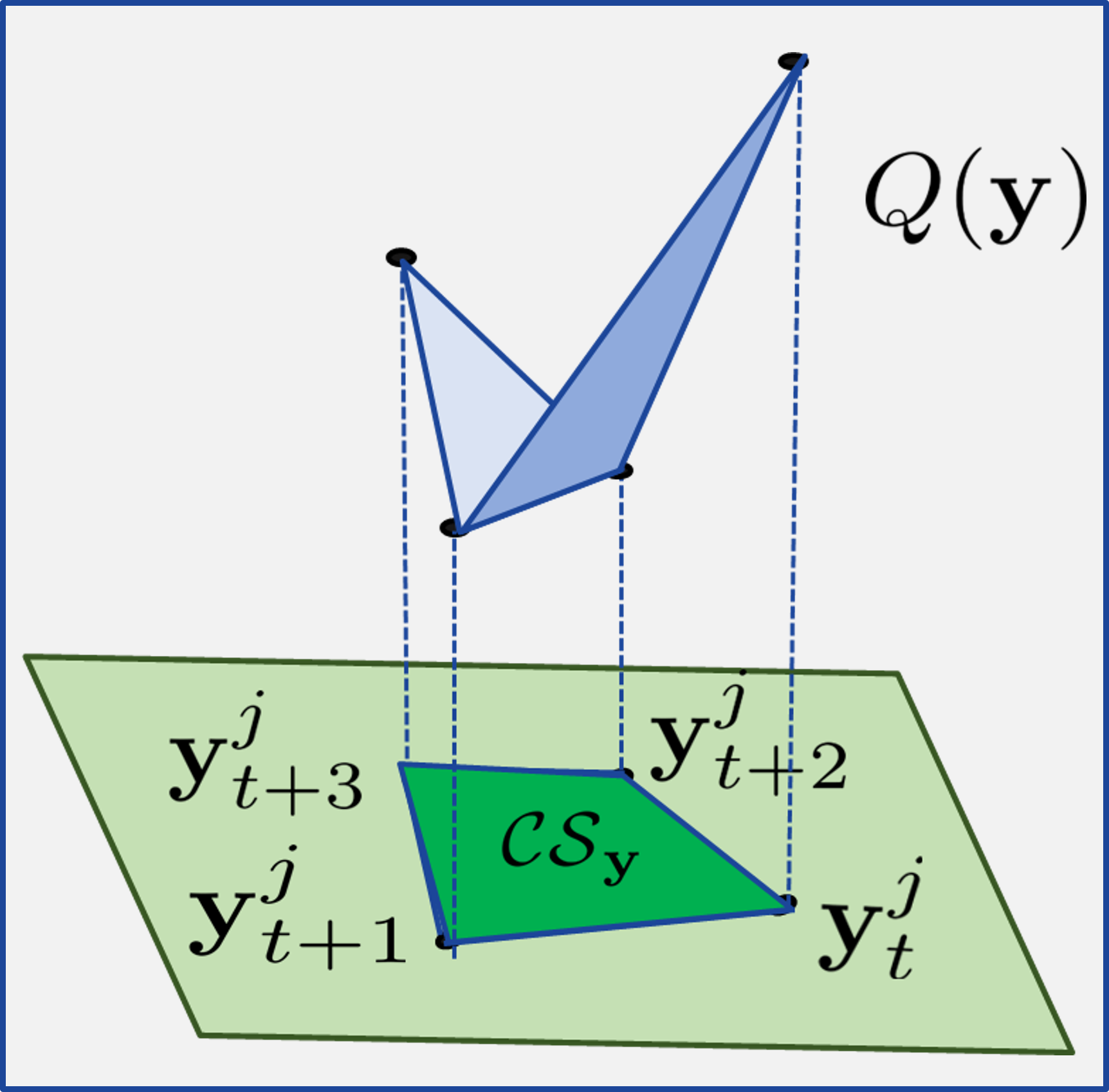
Towards performance, we propose a convex value function representation for flat nonlinear systems defined over convex safe sets in the space of output sequences. The value function and the safe set can be constructed from historical system trajectory data. We show that the output sequences in this safe set map to state and inputs within constraints. Moreover, we provide iterative performance improvement guarantees for the closed-loop system trajectories by using the value function approximation in our MPC design: Output-lifted Learning Model Predictive Control (OLMPC).
The two ideas presented above culminated in Robust Output-lifted LMPC (ROLMPC), which was recently implemented on the Berkeley Autonomous Racing Car (BARC) in collaboration with Edward Zhu: