On this page, we highlight our work on efficient, non-conservative collision avoidance in the presence of multi-modal predictions of traffic vehicles, for autonomous driving.

Our main theoretical contributions include:

(1) Robust, Stochastic and Distributionally Robust MPC formulations that optimize over a novel feedback policy class designed to exploit additional structure in the multi-modal predictions, and that is amenable to convex programming .

On the left, the ego vehicle plans using open-loop predictions. On the right, the ego vehicle plans using multi-modal policies

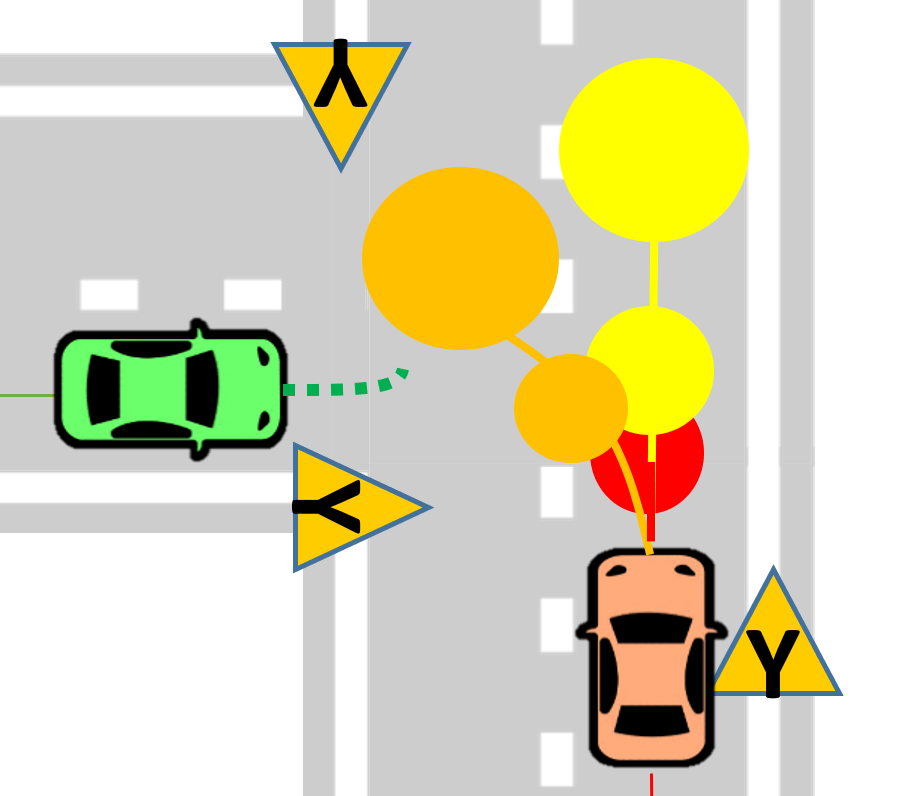
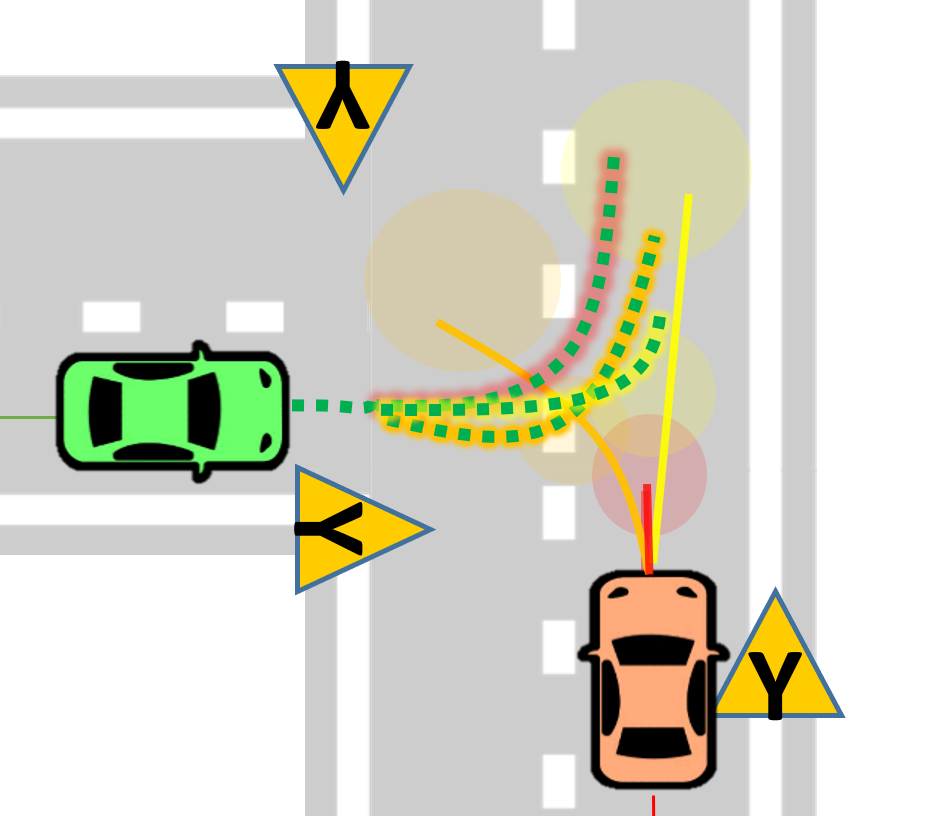
The use of feedback policies for prediction is motivated by the need for reduced conservatism in handling multi-modal predictions of the surrounding vehicles, especially prevalent in urban driving scenarios.

Multi-modal collision avoidance for an unprotected left turn in CARLA.

(2) Convexified, optimization-based collision avoidance between convex sets in the presence of uncertainty.

On the left, typical vehicle geometry representations. On the right, an illustration of separating hyperplanes found by the MPC algorithm

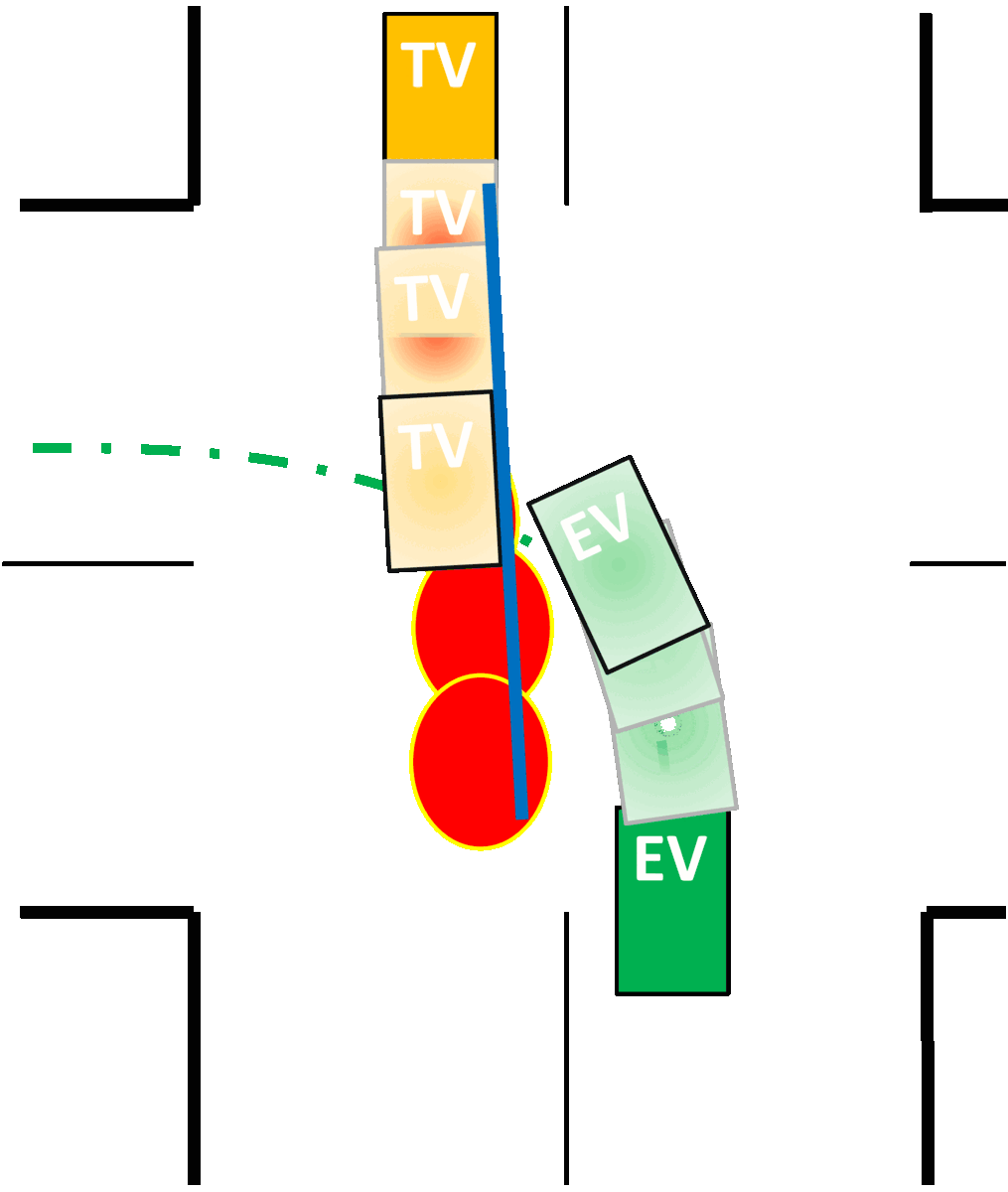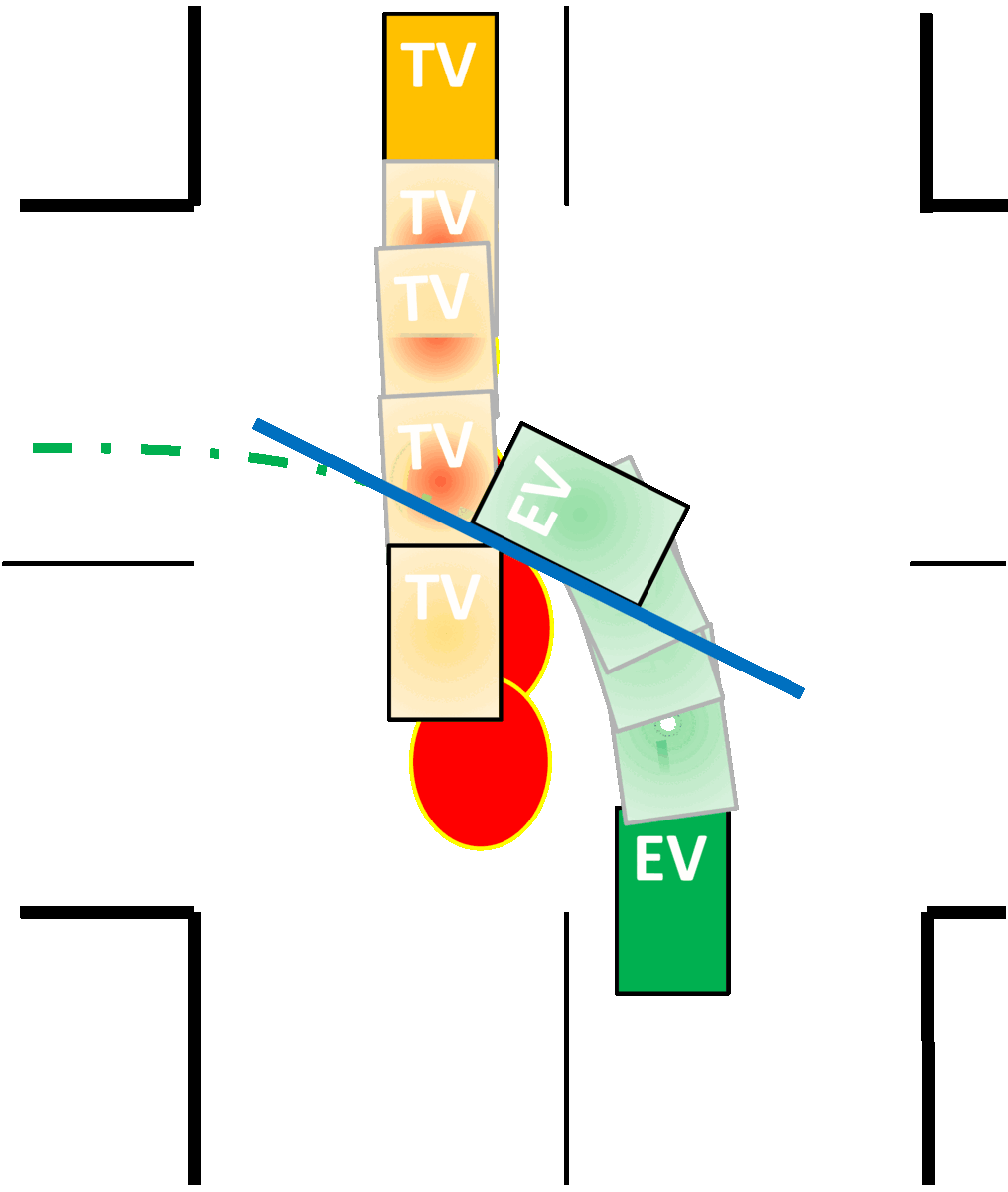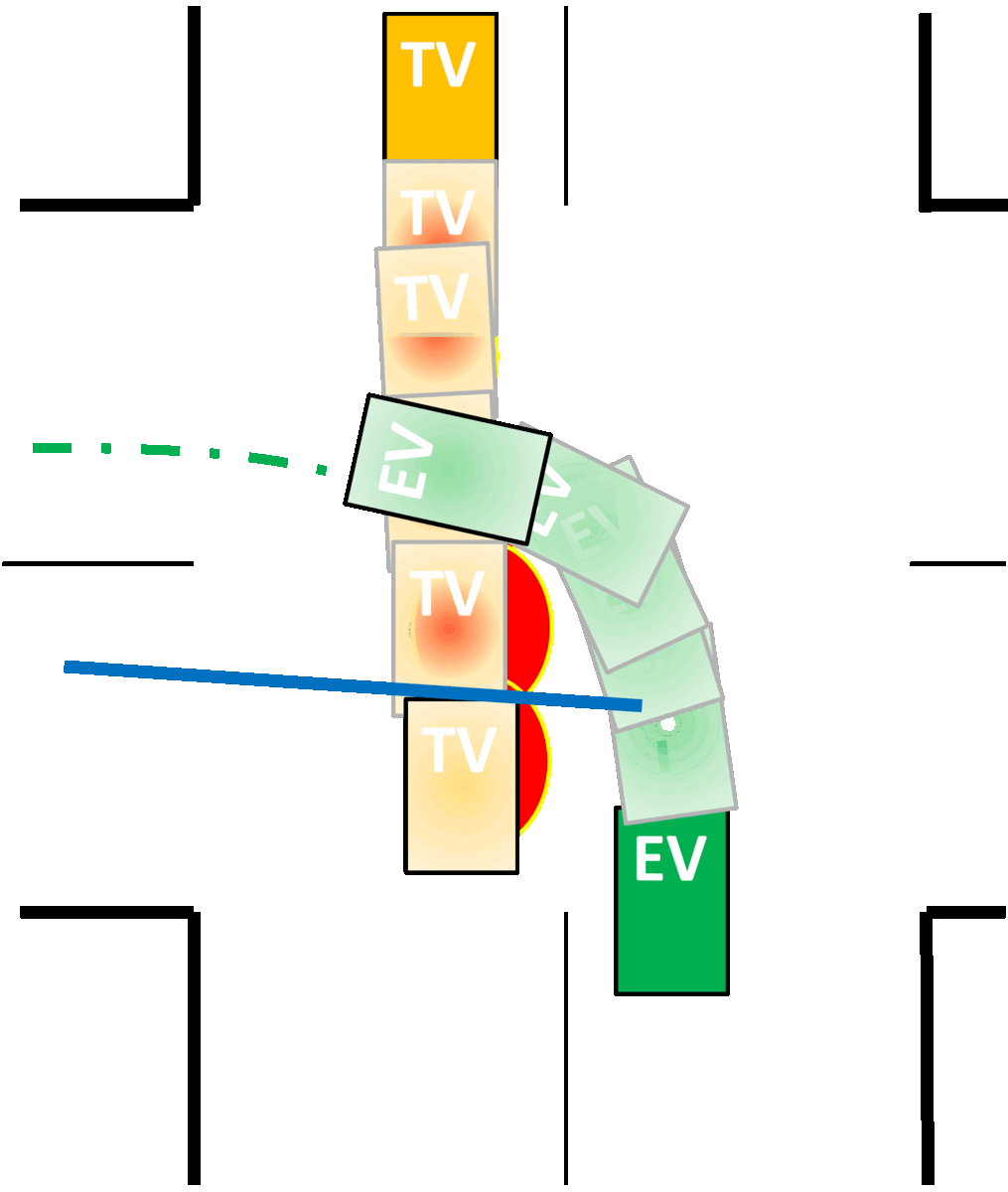
Collision avoidance constraints in the presence of uncertainty, are typically imposed by conservatively approximating the vehicle geometry as a (i) point, (ii) affine space, (iii) spheres or (iv) ellipsoids, instead of using polytopes to avoid non-smooth constraints. We use the dual perspective of collision avoidance to find separating hyperplanes between vehicles expressed as polytopes, while simulatenously accounting for the uncertainty in their locations.

We compare the separating hyperplane optimization approach, with the conventional, ellipsoidal approximation approach. We see that the former produces tighter turns even in the presence of uncertainty.

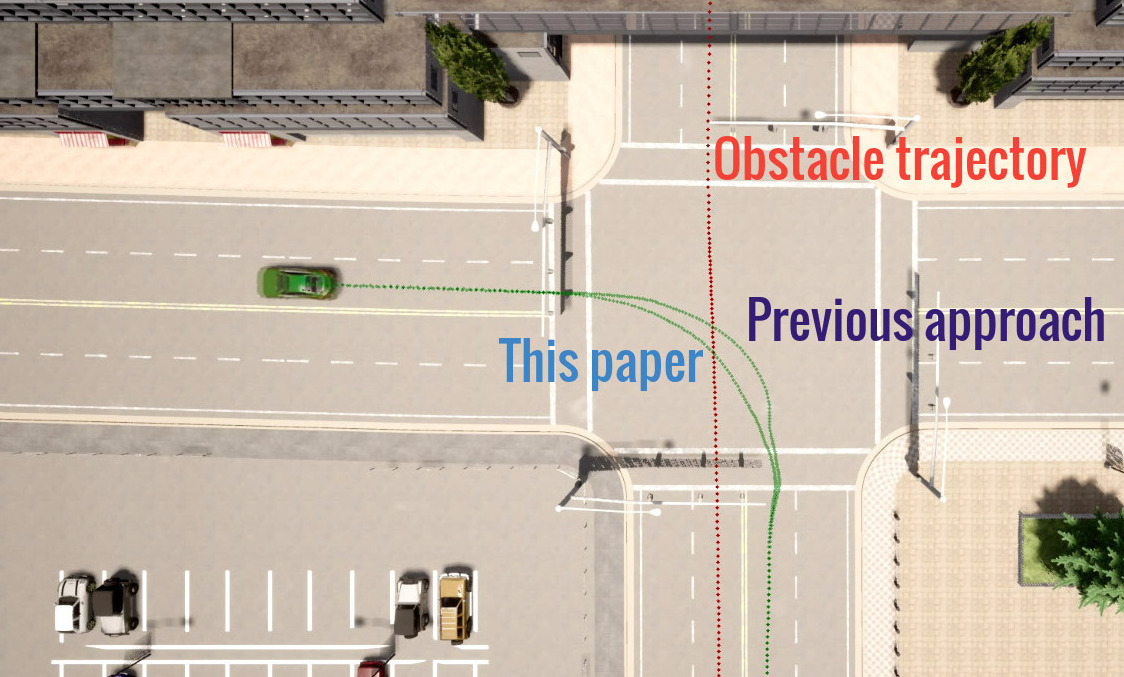
For more details, please see our papers from ITSC’22 and CDC’22.

Upcoming:

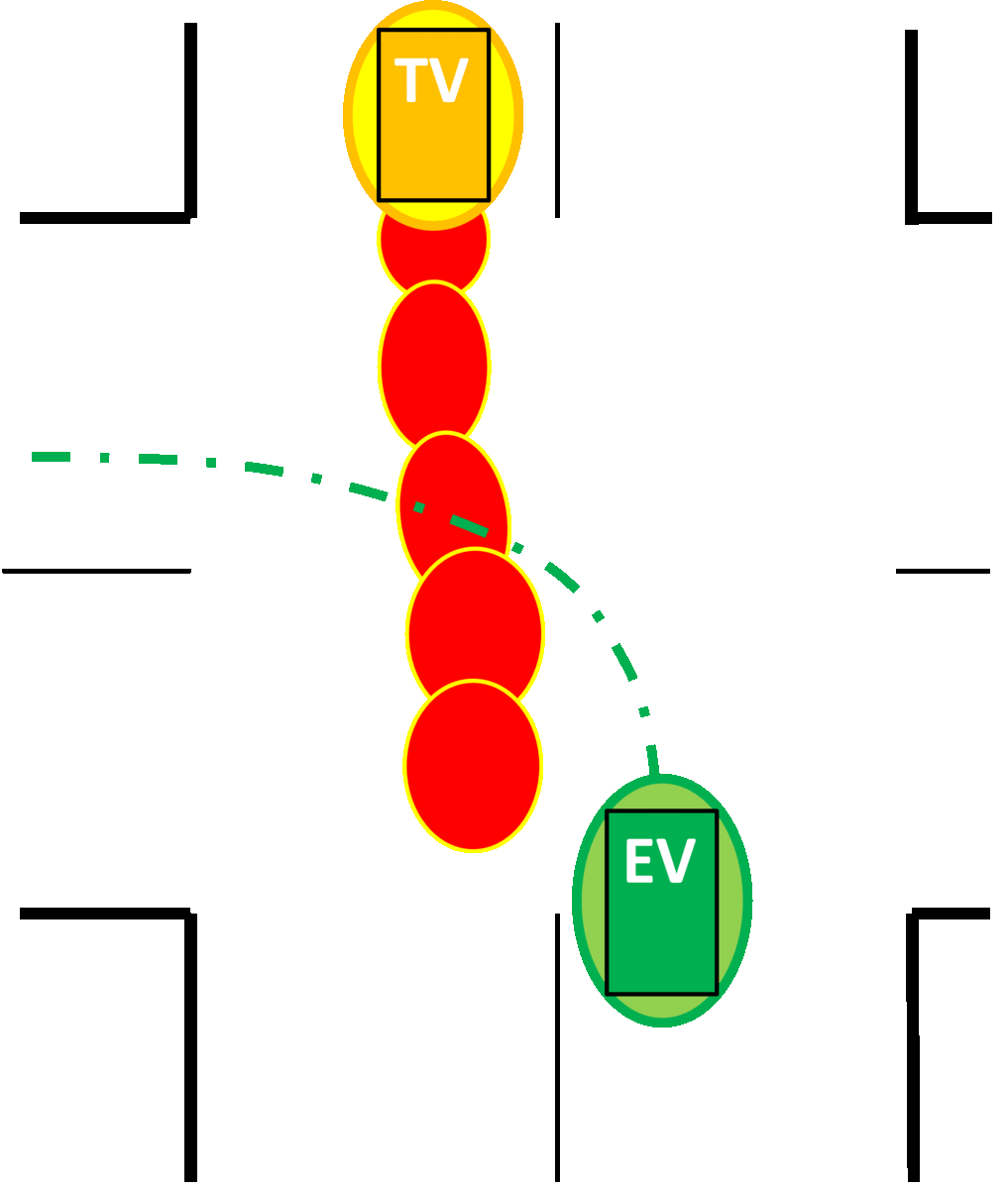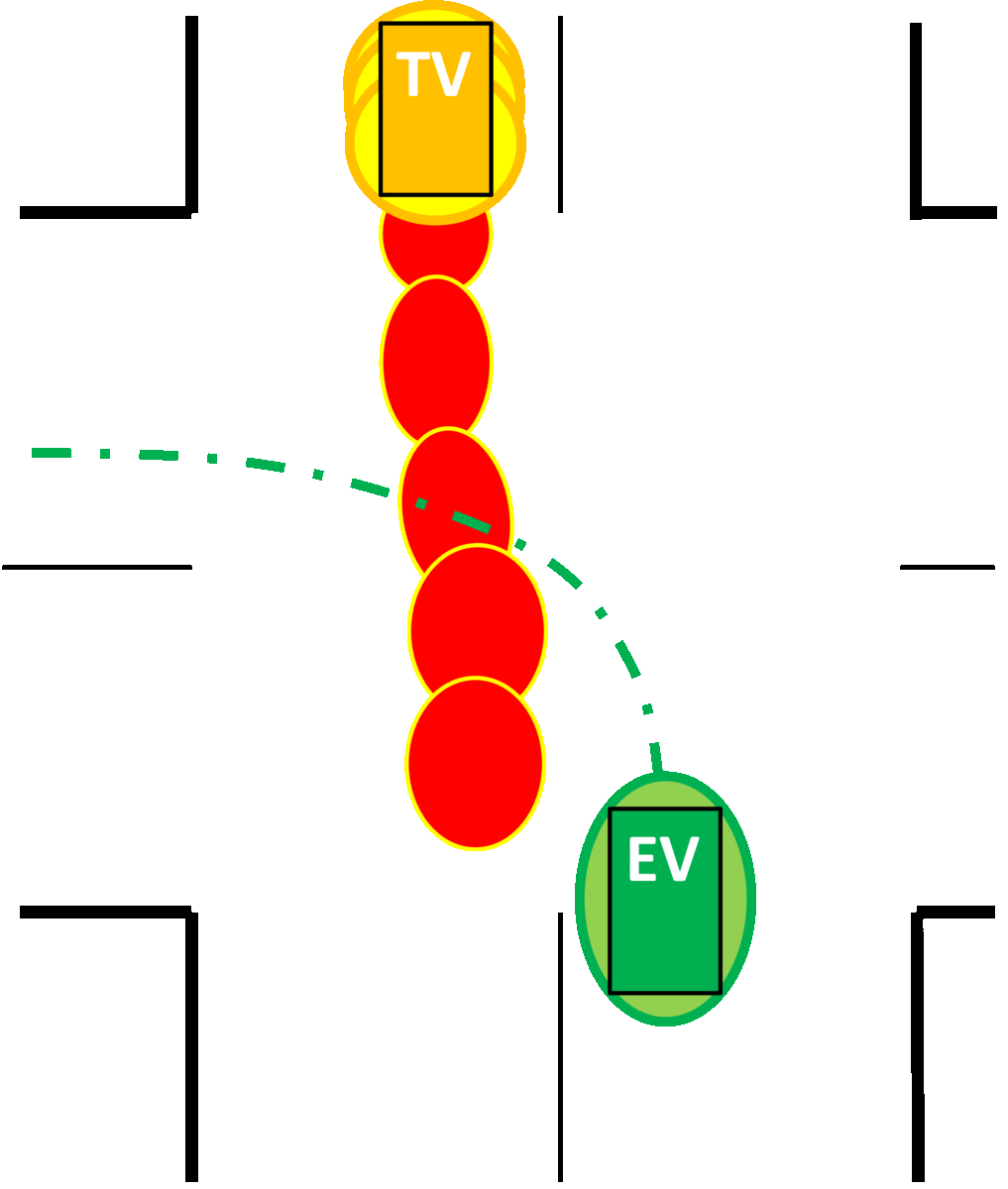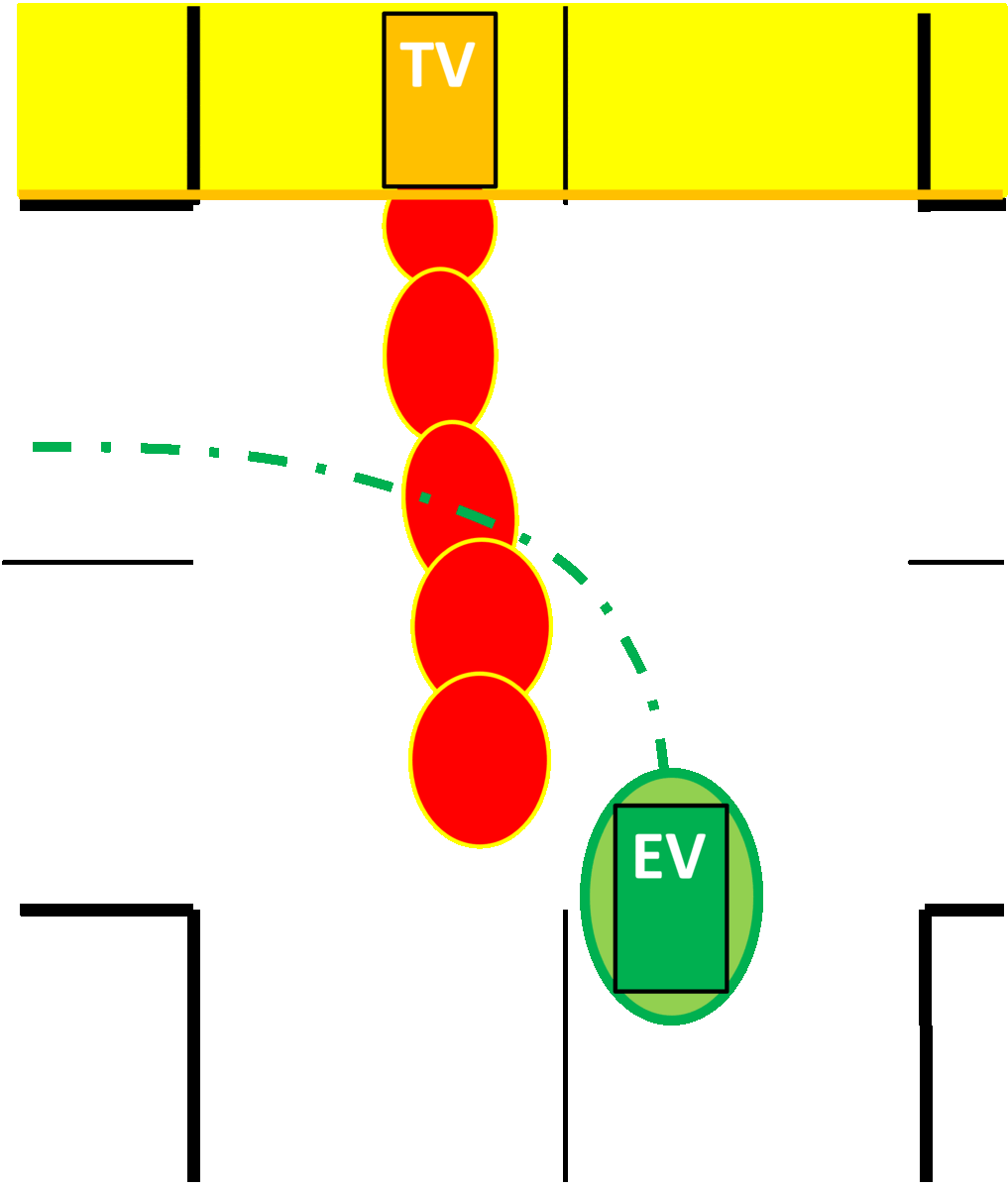
In addition to using multi-modal policies, we derive a convex formulation for simulataneous risk allocation and optimization of policies for multi-modal obstacle avoidance constraints. The figure below underscores the importance of this contribution. For \(x\) given by a Gaussian mixture (where \(x\) could denote the distance between vehicles), the figure depicts two formulations for shaping its multi-modal distribution via the means \(\mu\) to satisfy \(\mathbb{P}(x>0)\geq p^\star\).

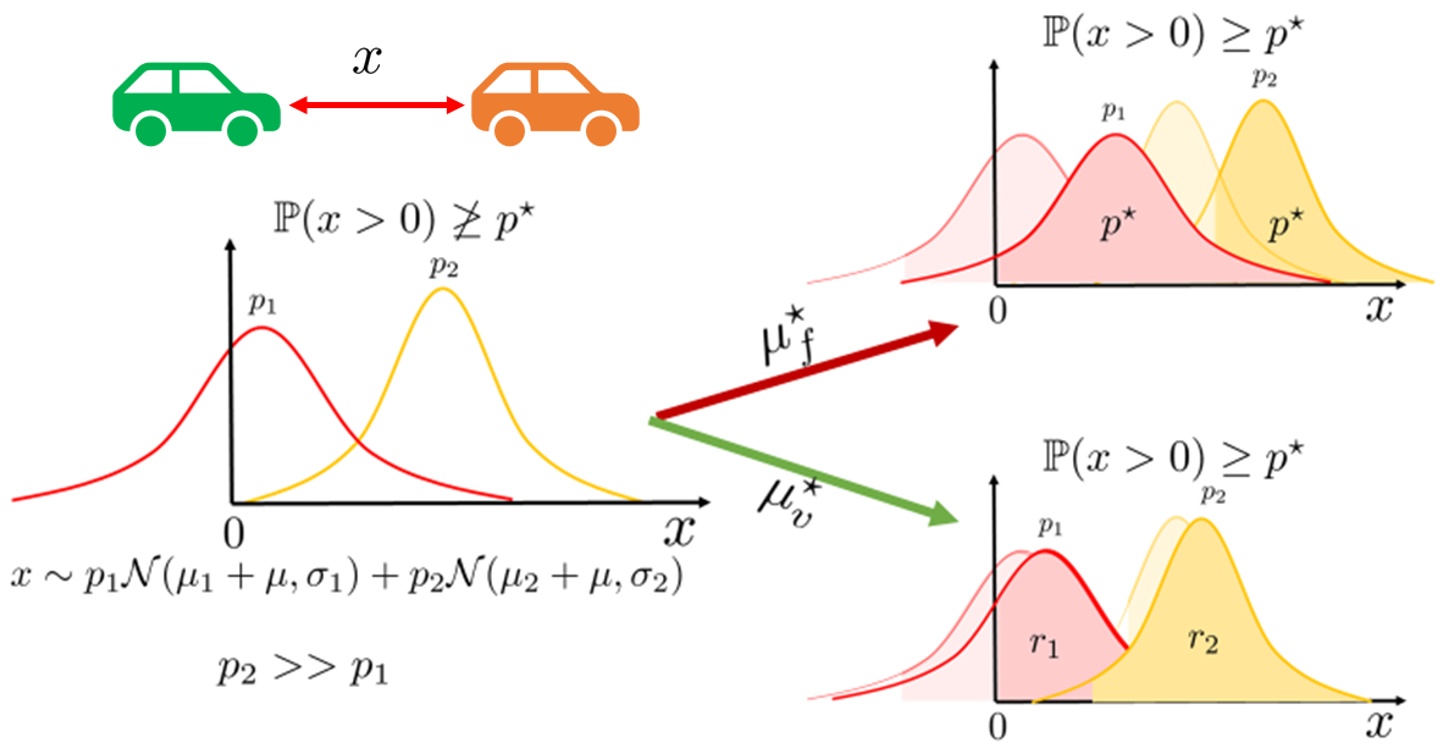
The resulting distributions are shown on the right for the uniform risk and variable risk allocation formulations at the top and bottom respectively. The latter allows satisfaction of the chance constraint without agressive shaping of the distribution, by exploiting the difference in probabilities of the modes. Consequently, this improves the feasibility of MPC optimization problems by allocating less risk to unlikely modes, without compromising on safety! This approach was recently developed and implemented on a full-scale vehicle in collaboration with Hotae Lee and Eunhyek Joa:

Autonomous lane change at the Richmond Field Station in the presence of two virtual vehicles, with bi-modal predictions. The experimental setup is largely based on Joa*, Lee* et al., IV'23.

The technical details will be available soon. Stay tuned!