publications

2023

1. IV

   Interaction and Decision Making-aware Motion Planning using Branch Model Predictive Control

   Rui Oliveira, Siddharth H. Nair, and Bo Wahlberg

   In 2023 IEEE Intelligent Vehicles Symposium

   Abs URL

   Motion planning for autonomous vehicles sharing the road with human drivers remains challenging. The difficulty arises from three challenging aspects: human drivers are 1) multimodal, 2) interacting with the autonomous vehicle, and 3) actively making decisions based on the current state of the traffic scene. We propose a motion planning framework based on Branch Model Predictive Control to deal with these challenges. The multimodality is addressed by considering multiple future outcomes associated with different decisions taken by the human driver. The interactive nature of humans is considered by modeling them as reactive agents impacted by the actions of the autonomous vehicle. Finally, we consider a model developed in human neuroscience studies as a possible way of encoding the decision making process of human drivers. We present simulation results in various scenarios, showing the advantages of the proposed method and its ability to plan assertive maneuvers that convey intent to humans.

2. 

   ×

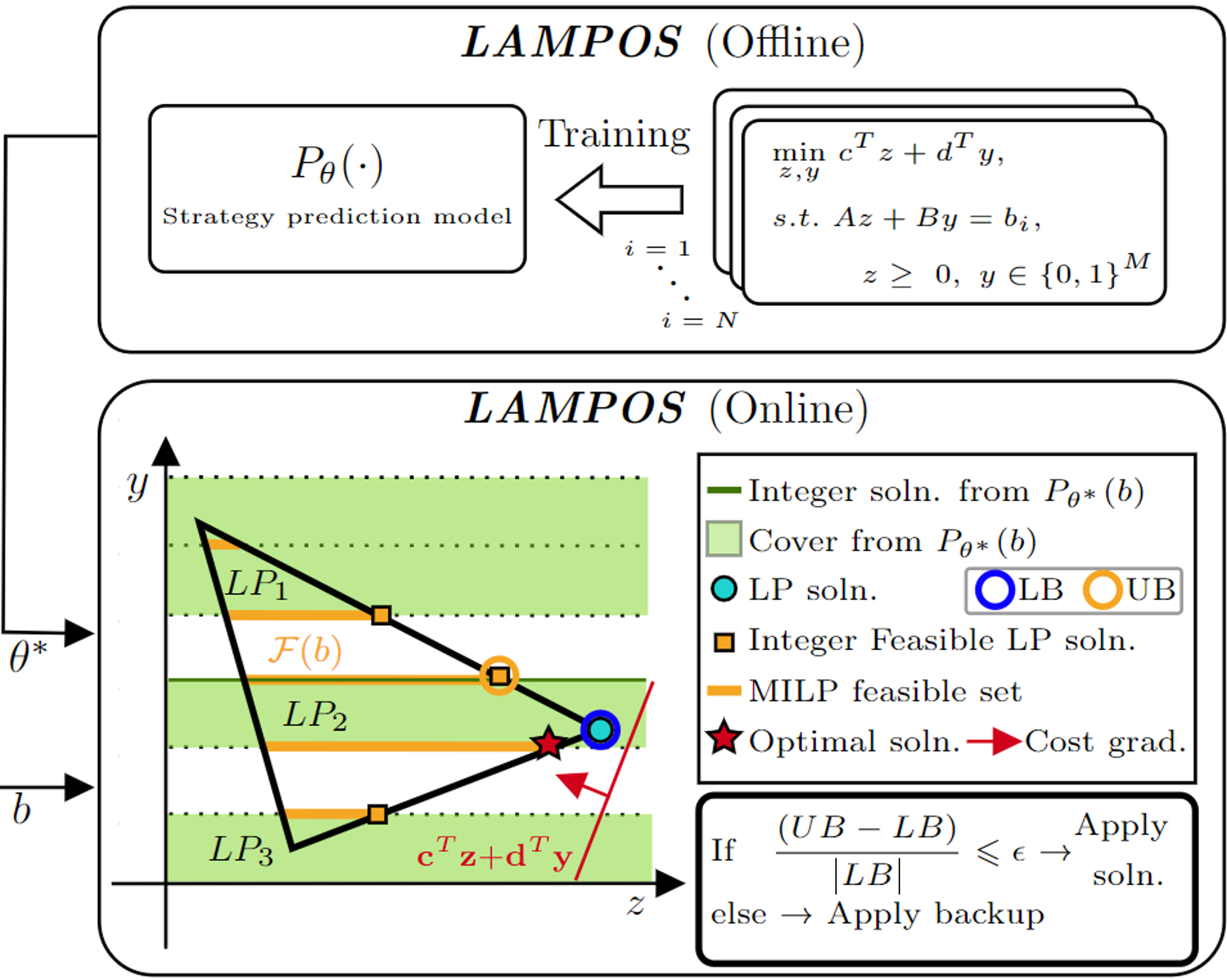
   Learning for Online Mixed-Integer Model Predictive Control with Parametric Optimality Certificates

   Luigi Russo*, Siddharth H. Nair*, Luigi Glielmo, and Francesco Borrelli

   IEEE Control Systems Letters, 2023

   Abs arXiv Code

   We propose a supervised learning framework for computing solutions of multi-parametric Mixed Integer Linear Programs (MILPs) that arise in Model Predictive Control. Our approach also quantifies sub-optimality for the computed solutions. Inspired by Branch-and-Bound techniques, the key idea is to train a Neural Network/Random Forest, which for a given parameter, predicts a strategy consisting of (1) a set of Linear Programs (LPs) such that their feasible sets form a partition of the feasible set of the MILP and (2) a candidate integer solution. For control computation and sub-optimality quantification, we solve a set of LPs online in parallel. We demonstrate our approach for a motion planning example and compare against various commercial and open-source mixed-integer programming solvers.

3. 

   ×

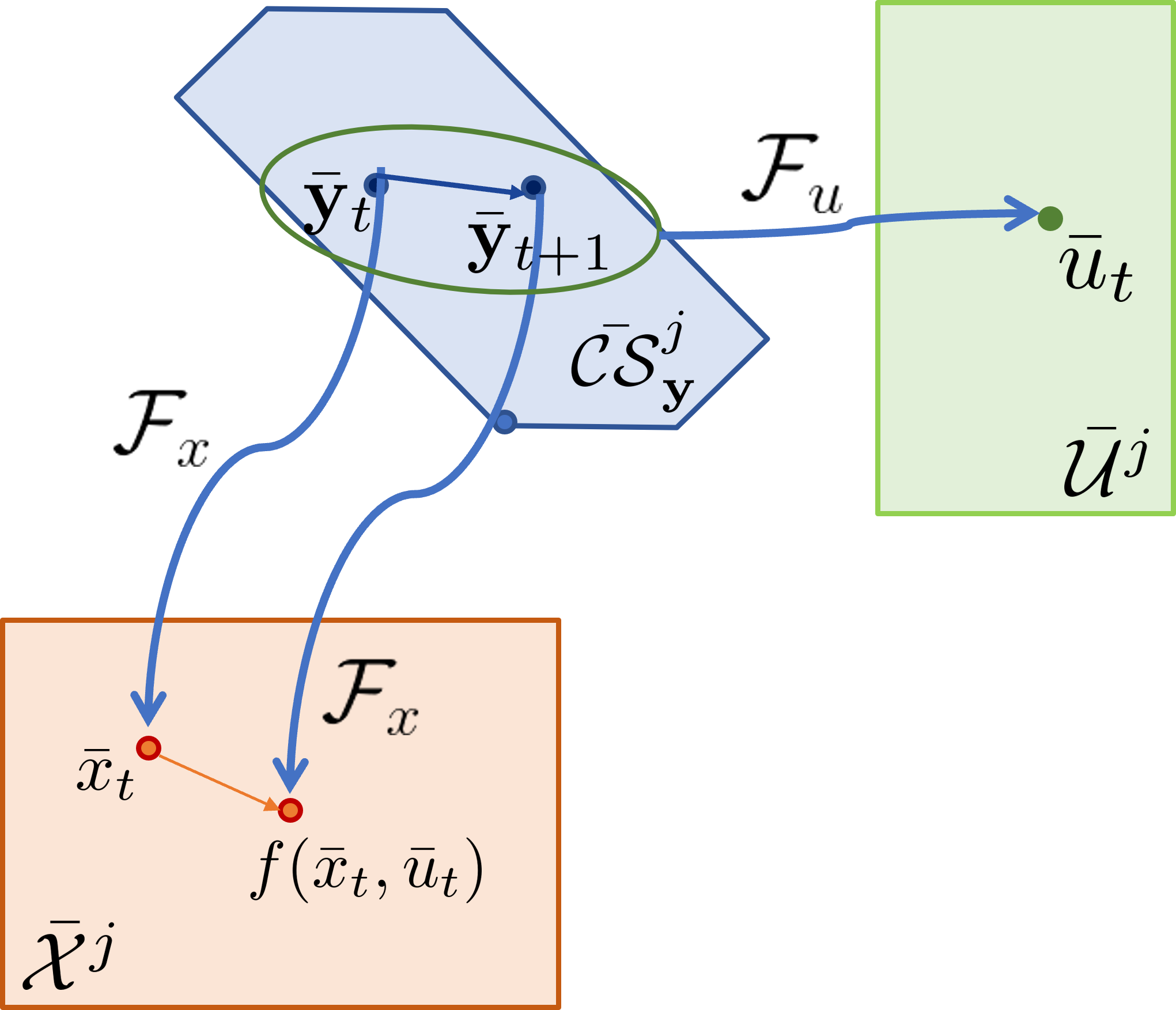
   Robust Output-Lifted Learning Model Predictive Control

   Siddharth H. Nair, and Francesco Borrelli

   arXiv preprint arXiv:2303.12127, 2023

   Abs arXiv Code

   We propose an iterative approach for designing Robust Learning Model Predictive Control (LMPC) policies for a class of nonlinear systems with additive, unmodelled dynamics. The nominal dynamics are assumed to be difference flat, i.e., the state and input can be reconstructed using flat output sequences. For the considered class of systems, we synthesize Robust MPC policies and show how to use historical trajectory data collected during iterative tasks to 1) obtain bounds on the unmodelled dynamics and 2) construct a convex value function approximation along with a convex safe set in the space of output sequences for designing terminal components in the Robust MPC design. We show that the proposed strategy guarantees robust constraint satisfaction, asymptotic convergence to a desired subset of the state space, and non-decreasing closed-loop performance at each policy update. Finally, simulation results demonstrate the effectiveness of the proposed strategy on a minimum time control problem using a constrained nonlinear and uncertain vehicle model.

2022

1. ITSC

   Stochastic mpc with multi-modal predictions for traffic intersections

   Siddharth H. Nair*, Vijay Govindarajan*, Theresa Lin, Chris Meissen, and 2 more authors

   In 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC)

   Abs URL Code

   We propose an Adaptive MPC framework for uncertain linear systems to achieve robust satisfaction of state and input constraints. The uncertainty in the system is assumed additive, state dependent, and globally Lipschitz with a known Lipschitz constant. We use a non-parametric technique for online identification of the system uncertainty by approximating its graph via envelopes defined by quadratic constraints. At any given time, by solving a set of convex optimization problems, the MPC controller guarantees robust constraint satisfaction for the closed-loop system for all possible values of system uncertainty modeled by the envelope. The uncertainty envelope is refined with data using Set Membership Methods. We highlight the efficacy of the proposed framework via a detailed numerical example.

2. CDC

   Collision avoidance for dynamic obstacles with uncertain predictions using model predictive control

   Siddharth H. Nair, Eric H. Tseng, and Francesco Borrelli

   In 2022 IEEE 61st Conference on Decision and Control (CDC)

   Abs URL Code

   We propose a Model Predictive Control (MPC) for collision avoidance between an autonomous agent and dynamic obstacles with uncertain predictions. The collision avoidance constraints are imposed by enforcing positive distance between convex sets representing the agent and the obstacles, and tractably reformulating them using Lagrange duality. This approach allows for smooth collision avoidance constraints even for polytopes, which otherwise require mixed-integer or non-smooth constraints. We consider three widely used descriptions of the uncertain obstacle position: 1) Arbitrary distribution with polytopic support, 2) Gaussian distributions and 3) Arbitrary distribution with first two moments known, and obtain deterministic reformulations of the collision avoidance constraints. The proposed MPC formulation optimizes over feedback policies to reduce conservatism in satisfying the collision avoidance constraints. The proposed approach is validated using simulations of traffic intersections in CARLA.

3. AVEC

   Stochastic mpc with dual control for autonomous driving with multi-modal interaction-aware predictions

   Siddharth H. Nair, Vijay Govindarajan, Theresa Lin, Yan Wang, and 2 more authors

   In International Symposium on Advanced Vehicle Control (AVEC) , 2022

   Abs URL Code

   We propose a Stochastic MPC (SMPC) approach for autonomous driving which incorporates multimodal, interaction-aware predictions of surrounding vehicles. For each mode, vehicle motion predictions are obtained by a control model described using a basis of fixed features with unknown weights. The proposed SMPC formulation finds optimal controls which serves two purposes: 1) reducing conservatism of the SMPC by optimizing over parameterized control laws and 2) prediction and estimation of feature weights used in interaction-aware modeling using Kalman filtering. The proposed approach is demonstrated on a longitudinal control example, with uncertainties in predictions of the autonomous and surrounding vehicles.

4. 

   ×

   Control of Uncertain PWA Systems using Difference-of-Convex Decompositions

   Siddharth H. Nair, and Yvonne R. Stürz

   2022

   Abs URL arXiv

   In this work, we analyse and design feedback policies for discrete-time Piecewise-Affine (PWA) systems with uncertainty in both the affine dynamics and the polytopic partition. The main idea is to utilise the Difference-of-Convex (DC) decomposition of continuous PWA systems to derive quadratic Lyapunov functions as stability certificates and stabilizing affine policies in a higher dimensional space. When projected back to the state space, we obtain time-varying PWQ Lyapunov functions and time-varying PWA feedback policies.

2021

1. NMPC

   Output-lifted learning model predictive control

   Siddharth H. Nair, Ugo Rosolia, and Francesco Borrelli

   IFAC-PapersOnLine, 2021

   Abs URL

   We propose a computationally efficient Learning Model Predictive Control (LMPC) scheme for constrained optimal control of a class of nonlinear systems where the state and input can be reconstructed using lifted outputs. For the considered class of systems, we show how to use historical trajectory data collected during iterative tasks to construct a convex value function approximation along with a convex safe set in a lifted space of virtual outputs. These constructions are iteratively updated with historical data and used to synthesize predictive control policies. We show that the proposed strategy guarantees recursive constraint satisfaction, asymptotic stability and non-decreasing closed-loop performance at each policy update. Finally, simulation results demonstrate the effectiveness of the proposed strategy on a piecewise affine (PWA) system, kinematic unicycle and bilinear DC motor.

2020

1. ECC

   A semi-definite programming approach to robust adaptive MPC under state dependent uncertainty

   Monimoy Bujarbaruah*, Siddharth H. Nair*, and Francesco Borrelli

   In 2020 European Control Conference (ECC)

   Abs URL

   We propose an Adaptive MPC framework for uncertain linear systems to achieve robust satisfaction of state and input constraints. The uncertainty in the system is assumed additive, state dependent, and globally Lipschitz with a known Lipschitz constant. We use a non-parametric technique for online identification of the system uncertainty by approximating its graph via envelopes defined by quadratic constraints. At any given time, by solving a set of convex optimization problems, the MPC controller guarantees robust constraint satisfaction for the closed-loop system for all possible values of system uncertainty modeled by the envelope. The uncertainty envelope is refined with data using Set Membership Methods. We highlight the efficacy of the proposed framework via a detailed numerical example.

2. IFAC WC

   Modeling of dynamical systems via successive graph approximations

   Siddharth H. Nair, Monimoy Bujarbaruah, and Francesco Borrelli

   IFAC-PapersOnLine, 2020

   Abs URL

   A non-parametric technique for modeling of systems with unknown nonlinear Lipschitz dynamics is presented. The key idea is to successively utilize measurements to approximate the graph of the state-update function of the system dynamics using envelopes described by quadratic constraints. The proposed approach is then used for computing outer approximations of the state-update function using convex optimization. We highlight the efficacy of the proposed approach via a detailed numerical example.

2019

1. 

   ×

   Predictive control for chasing a ground vehicle using a UAV

   Jaeseung Byun*, Karan P. Jain*, Siddharth H. Nair*, Haoyun Xu*, and 1 more author

   2019

   Abs URL arXiv Code

   We propose a high-level planner for a multirotor to chase a ground vehicle, while simultaneously respecting various state and input constraints. Assuming a minimal kinematic model for the ground vehicle, we use data collected online to generate predictions for our planner within a model predictive control framework. Our solution is demonstrated, both via simulations and experiments on a stable quadcopter platform.

2. ACC

   Control synthesis for an underactuated cable suspended system using dynamic decoupling

   Siddharth H. Nair, Ravi N. Banavar, and DH Sanjeeva Maithripala

   In 2019 American Control Conference (ACC)

   Abs URL

   This article studies the dynamics and control of a novel underactuated system: a ball and plate system suspended by a team of quadrotors via cables. The plate is sought to be horizontally stabilized at a certain height, with the ball stabilized at the center of mass of the plate. The freely moving ball adds 2 degrees of underactuation to the system. The design proceeds through a decoupling of the quadrotors and the plate dynamics. Through a partial feedback linearization approach, the attitude of the plate and the translational height of the plate is initially controlled, while maintaining a bounded velocity along the y and x directions. These inputs are then synthesized through the quadrotors with a backstepping and timescale separation argument based on Tikhonov’s theorem.

3. NOLCOS

   Discrete optimal control of interconnected mechanical systems

   Siddharth H. Nair, and Ravi N. Banavar

   11th IFAC Symposium on Nonlinear Control Systems, 2019

   URL

2017

1. CDC

   Hilbert’s space-filling curve for regions with holes

   Siddharth H. Nair, Arpita Sinha, and Leena Vachhani

   In 2017 IEEE 56th annual Conference on decision and control (CDC)

   Abs URL

   The paper presents a systematic strategy for implementing Hilbert’s space filling curve for use in online exploration tasks and addresses its application in scenarios wherein the space to be searched obstacles (or holes) whose locations are not known a priori. Using the self-similarity and locality preserving properties of Hilbert’s space filling curve, a set of evasive maneuvers are prescribed and characterized for online implementation. Application of these maneuvers in the case of non-uniform coverage of spaces and for obstacles of varying sizes is also presented. The results are validated with representative simulations demonstrating the deployment of the approach.

2. AAS/AIAA

   Attitude control of spacecraft formations subject to distributed communication delays

   Siddharth H. Nair, and Kamesh Subbarao

   In 27th AAS/AIAA Space Flight Mechanics Meeting 2017

   Abs URL

   This paper considers the problem of achieving attitude consensus in spacecraft formations with bounded, time-varying communication delays between spacecraft connected as specified by a strongly connected topology. A state feedback controller is proposed and investigated using a time domain approach (via LMIs) and a frequency domain approach (via the small-gain theorem) to obtain delay dependent stability criteria to achieve the desired consensus. Simulations are presented to demonstrate the application of the strategy in a specific scenario.